Neuland CTF 2023 Winter - Cryptography

December 9, 2023 Neuland CTF

Download challenges: Neuland CTF Repository

Secrets - Easy

Part 1: aynaq{o4f3
Part 2: ..--.- -.... ....- ..--.- .---- ..... ..--.- -. --- --... ..--.- ....- ..--.-
Part 3: M05DcllwNzFvbn0=

We get three parts of the flag encrypted/encoded by different methods. The first part of the message appears to represent nland{. The fact that { remains the same and the two Ns have been converted to As indicates a shift cipher. The string is ROT 13 encoded; it simply substitutes a letter with the 13th letter after in the alphabet. The second part consists exclusively of dots and dashes, indicating Morse code, which encodes text with two different signal durations. The last part is Base64, a binary-to-text encoding indicated by the = at the end of the sequence used as padding.

The flag is nland{b4s3_64_15_NO7_4_3NCrYp71on}

Hash - Easy

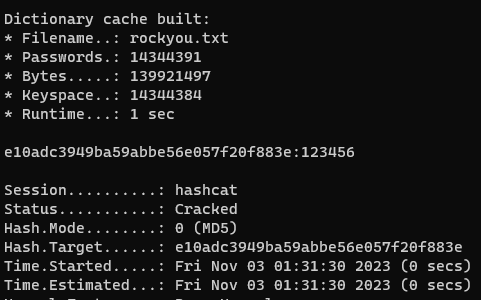
MD5: e10adc3949ba59abbe56e057f20f883e
SHA1: 5baa61e4c9b93f3f0682250b6cf8331b7ee68fd8
LM: 598DDCE2660D3193AAD3B435B51404EE

Flag format: nland{<MD5>_<SHA1>_<LM>} in all lowercase

The flag can be generated by brute forcing three different hashing algorithms. A hash is a digital fingerprint that uses a hash function to map data of any length to a shorter, fixed-length value. In IT security, these hashes are mostly one-way functions and offer collision resistance, making it easy to calculate a hash but almost impossible to conclude the original string. Therefore, an efficient way to decrypt the hashes is a dictionary attack, where frequently used words are hashed with the respective hashing algorithm and compared with the original. Tools like hashcat make this process easy. We download a dictionary like rockyou.txt and use it as input for hashcat. The command looks like the following:

hashcat.exe -a 0 -m 0 hash.txt rockyou.txt
hashcat.exe -a 0 -m 100 hash.txt rockyou.txt
hashcat.exe -a 0 -m 3000 hash.txt rockyou.txt

The hash.txt file contains the hash value to be decrypted. We use the parameter -a to determine the dictionary mode, -m stands for the hash algorithm.

The flag is nland{123456_password_qwerty}

Baby - Easy

Can you read my message without the private key?

c: 24795976732186127960014008753803478286219924961358994925564930277505139413283367757656447224830225064133651246343035441112407129772003927463166449052456907513
e: 65537
n: 67037366790941822378007197878613492487588187468048328737227273255156041659689092651657208107757810805499108569166854436320366276808520739379431210884782583791

The title already reveals that it is about the cryptographic method RSA. Since n only has 158 digits, we have a good chance of finding the two factors, q and p, needed to calculate the private key. FactorDB is an online collection of prime numbers which fortunately stores our fully factored n. The private key d can be calculated with inverse(e) % (p-1) * (q-1). With the private key, the ciphertext c can be decrypted with the equation M = pow(C , d) % n.

Python script:

from Crypto.Util.number import *

p = 7796601204626807
q = 8598280844627430267706791405975187760390046230909096659417881790296619284204527797467017995321195814866230752519838250409205362581256112387913
n = 67037366790941822378007197878613492487588187468048328737227273255156041659689092651657208107757810805499108569166854436320366276808520739379431210884782583791
c = 24795976732186127960014008753803478286219924961358994925564930277505139413283367757656447224830225064133651246343035441112407129772003927463166449052456907513
e = 65537

d = inverse(e,(p-1)*(q-1))
m = pow(c,d,p*q)
print("Message: ", long_to_bytes(m))

The flag is nland{ROll1n9_your_Own_r54}

All the Colors of Christmas - Medium

Santa has a message for you.
(Flag format nland{<message>} in all lowercase)

An LED-illuminated Christmas tree is provided to solve the task, which regularly changes its colors. After looking at it for a while, the following features become apparent:

6 different colors (green, yellow, blue, light blue, pink, red)
The 6th color is displayed longer
After 18 colors, the Christmas tree shuts down and starts again from the beginning

With this information, we can create the following pattern:


green	yellow	yellow	blue	green	yellow	yellow	blue
red	blue	light blue	pink	red	blue	light blue	pink
light blue	pink	green	red	light blue	pink	green	red

A quick Google search shows that only a few cryptographic algorithms use colors as a form of representation. One of them is Hexahue, which uses the same colors.

Enter the color combination into an online decoder and get the word ho.

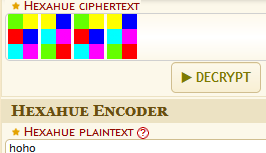
The flag is nland{hoho}